Posts
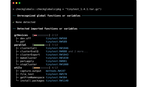
Multistart nonlinear least squares fitting with {gslnls}
Introduction When fitting a nonlinear regression model in R with nls(), the first step is to select an appropriate regression model to fit the observed data, the second step is to find reasonable starting values for the model parameters in order to initialize the nonlinear least-squares (NLS) algorithm.
New nonlinear least squares solvers in R with {gslnls}
Introduction Solving a nonlinear least squares problem consists of minimizing a least squares objective function made up of residuals \(g_1(\boldsymbol{\theta}), \ldots, g_n(\boldsymbol{\theta})\) that are nonlinear functions of the parameters of interest \(\boldsymbol{\theta} = (\theta_1,\ldots, \theta_p)'\):
Mesmerizing multi-scale Turing patterns in R with Rcpp
This post showcases several multi-scale Turing patterns generated in R with Rcpp(Armadillo). The generating process, inspired by (McCabe 2010), consists of multi-scale convolutions with respect to short-range activator kernels and long-range inhibitor kernels, computed efficiently in the Fourier domain using RcppArmadillo. Starting from an almost homogeneous state, the algorithm generates regular 2D Turing patterns with smoothly varying behavior across multiple scales that are quite fascinating to look at.
Automatic differentiation in R with Stan Math
Introduction Automatic differentiation Automatic differentiation (AD) refers to the automatic/algorithmic calculation of derivatives of a function defined as a computer program by repeated application of the chain rule. Automatic differentiation plays an important role in many statistical computing problems, such as gradient-based optimization of large-scale models, where gradient calculation by means of numeric differentiation (i.
GSL nonlinear least squares fitting in R
Introduction The new gslnls-package provides R bindings to nonlinear least-squares optimization with the GNU Scientific Library (GSL) using the trust region methods implemented by the gsl_multifit_nlinear module. The gsl_multifit_nlinear module was added in GSL version 2.
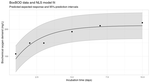
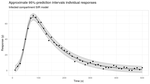
Asymptotic confidence intervals for NLS regression in R
Introduction Nonlinear regression model As a model setup, we consider noisy observations \(y_1,\ldots, y_n \in \mathbb{R}\) obtained from a standard nonlinear regression model of the form:
\[ \begin{aligned} y_i &\ = \ f(\boldsymbol{x}_i, \boldsymbol{\theta}) + \epsilon_i, \quad i = 1,\ldots, n \end{aligned} \] where \(f: \mathbb{R}^k \times \mathbb{R}^p \to \mathbb{R}\) is a known nonlinear function of the independent variables \(\boldsymbol{x}_1,\ldots,\boldsymbol{x}_n \in \mathbb{R}^k\) and the unknown parameter vector \(\boldsymbol{\theta} \in \mathbb{R}^p\) that we aim to estimate.
Step function regression in Stan
Introduction The aim of this post is to provide a working approach to perform piecewise constant or step function regression in Stan. To set up the regression problem, consider noisy observations \(y_1, \ldots, y_n \in \mathbb{R}\) sampled from a standard signal plus i.